Competition and evolutionary-enlightened treatments: treatment (part 3)

From previous posts we now know that chemo-sensitive and chemo-resistant clones compete even when space is abundant and thus sensitive cells can be used to control the resistant population. We also know that in many, probably most cases, chemotherapy alone will not kill a tumour and that just “giving it all we got” is likely to expedite the emergence of resistant untreatable tumours. So, are Adaptive Therapies (ATs) so much better?

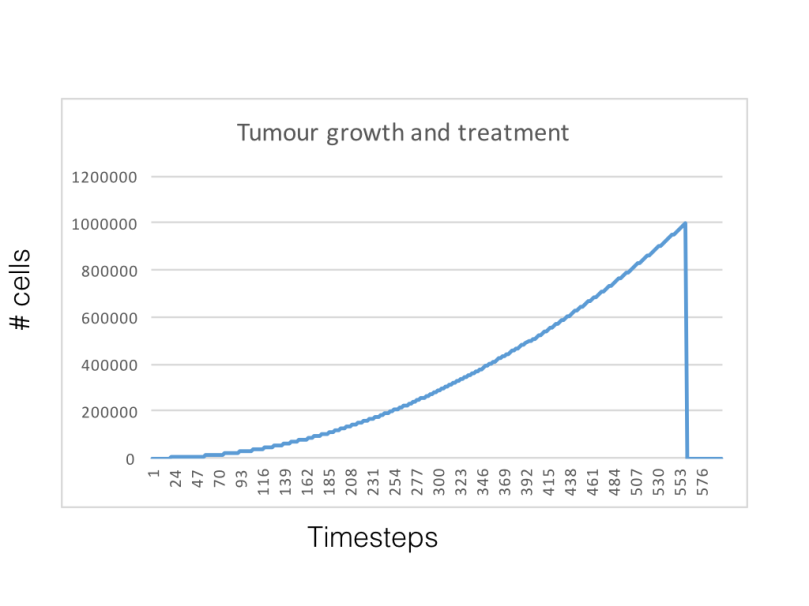
I have read a few slightly different implementations of ATs by the authors (CR 2009, Biol Direct 2010, CR 2012). The easiest definition of an AT involves the use of chemotherapy only as a way to control a population. Thus we will define a population size we want to achieve and some margin around which we can allow some wiggle. So let’s compare three simulations, one with no treatment, one with conventional lets-give-it-all chemo and one with an AT. The AT will aim to control the tumour population around the 100,000 cells mark and cease chemo when the population goes below 90,000. Here’s a simulation that shows how the AT approach works in this implementation:

 

As it is before, darker colors represent susceptible cells but as the cells display brighter colors (cyan->yellow->red) they become less susceptible.

And this plot compares the change in tumour population for the three different simulations (untreated, conventional chemo and AT):

The results show that not treating the tumor is clearly the worst of the options, that using chemotherapy in a conventional way can quickly select for resistance and that ATs could be a worthwhile alternative. The little insert on the top-left corner shows what happens when we run AT for longer. The Untreated and conventional treatments were run for about half the time that AT was, mostly because I could see what the result would be at the end. The effects of AT clearly do not last for ever and, if you look at the movie, it is easy to see why: every time the treatment is applied the overall phenotypic composition of the tumor shifts slightly towards more resistance.

Of course this has only scratched the surface of the issue. A more systematic and thorough comparison would allow us not only to be more certain about the advantages of ATs over conventional application of chemotherapy but also to say something about the importance of intra tumour heterogeneity in determining this.

Interestingly, mathematical models of AT typically assume resistance to be binary: either the cell is resistant (in which case it will resist any amount of chemo) or is not. I decided to try to see how AT would work on a version of the model where cells are either resistant or susceptible. I think the results suggest that AT would work better under this binary assumption which makes me think that ATs would work even better in treatments where evolution would have a less smooth landscape to operate on.

It is clear to many of us that ATs (and other evolutionary enlightened approaches such as evolutionary double binds) are likely to be more effective in many situations. The NCI has invested some good money to further explore this idea. Even a clinical trial is currently under way at Moffitt to test approaches based on AT in prostate cancer. But as we said on the first post of this series, the trade off is that we would need to consider cancer as a chronic disease and not something that could be cured once and for all. This would seem a reasonable compromise for a lot of patients but if we could find out more about which ones would do better with AT and which ones we can treat in a more definite way , that would be undoubtedly better. I expect that tumour heterogeneity (its origin and the mechanisms that maintain it) and a better understanding of the interactions with the microenvironment will be key for help us determine this. Expect some more thorough analysis discussing these points in a preprint server near you .

Competition and evolutionary-enlightened treatments: heterogeneity (part 2)

In the last post we discussed how the concept of Adaptive Therapies (ATs) depends critically on competition for resources between chemotherapy resistant cells and chemotherapy sensitive cells. This competition is what allows resistance to be kept in check when treatment is not applied. The balance between this competition and overall population growth is what drives the success of a good AT.

Here is an example of what happens when we apply chemotherapy in a conventional way, that is, the treatment is applied for as long as the overall tumor population responds to it. Take a look at the featured image in this post to have an idea of how the colors correspond to the number of pumps (that correlate with resistance and slow proliferation). In this simulation the mutation rate was set to 10% to allow for faster dynamics:

A longer version can be seen here but I only show the action every 50 time steps:

 

Here is how growth is affected shortly after the application of the treatment:

The plots show how as the chemotherapy is applied, the population initially decreases but, as the average number of pumps increase (which decrease proliferation but increase resistance to chemo)  the population becomes increasingly resistant. But is this resistance something that comes from a pre-existing population or does it evolve de novo? In the case of this model the answer is complicated. The following plot shows the evolution of the tumor size and its heterogeneity over time (in a different but equivalent simulation in a smaller grid so the number of cells is smaller) over time using a Shannon index:

I am not clear that the Shannon index is the best metric but it is widely accepted and will keep using it unless a reader comes with a better suggestion. The plot shows that heterogeneity increases initially but remains low for a time as selection goes for cells that resemble the phenotype the simulation was seeded with (with 1 pump). At timestep=1000 the treatment is applied and, even though population size is reduced, heterogeneity increases once again.

This begs the question: how sensitive are these results to the heterogeneity of the tumor at the time of application of chemotherapy? Heterogeneity explains why chemotherapy does not kill all the tumor cells, at least initially. In this model there are three sources of heterogeneity in the tumor population: 1. the mutation rate; 2. the strength of selection in the absence of chemotherapy (weak selection would explain the presence of resistant cells in the absence of treatment); and 3. the strength of selection during treatment (weak selection would give time to sensitive cells to produce progeny that might be more resistant). Let’s see now a simulation where we make it more difficult for the tumor to evolve resistance: starting only with sensitive cells, 1% mutation rate, higher cost for cells with pumps (stronger selection in the absence of treatment) and high chemo efficacy (stronger selection against sensitive cells in the presence of treatment).

Yay, this time the tumor did not have a chance! How does the Shannon index of  this simulation compare to the previous simulation? It is much smaller! It is about 0.71 (compared to close to 2.7 in the previous simulation).

So we can, at least in theory, treat our simulated tumors in a way that resistance will not emerge. But that requires us to focus on aspects of cancer evolution for which we have little or no control. More likely than not, efficacy of the treatment, delivery and even microenvironmental protection (see the work by Meads, Gatenby and Dalton at NRC for a comprehensive review) will increase the chances for resistance to emerge. So what happens when we allow for a section of the microenvironment (centered in the middle of the computational domain) to confer protection to the tumour cells, regardless of their sensitivity to chemotherapy?

It seems that in most occasions we can assume that hitting the computer simulated tumour as hard as we can with chemo might not be a great solution. What else can we do? I suspect you know what I will be suggesting in my next post but here is a hint:

 

 

Competition and evolutionary-enlightened treatments: competition (part 1)

Here at Moffitt we are privileged to work with physician-scientists like Bob Gatenby that understands and encourages the use of mathematical modeling in cancer. It is his effort, after all, that made our department of Integrated Mathematical Oncology possible in the first place.

One of the ideas that Bob has been championing is called Adaptive Therapies (AT). This approach (explained in Gatenby et al CR 2009 and Silva et al CR 2012) means that instead of trying to kill all the tumor cells we can with standard treatments like chemotherapy, we should instead aim to just kill as many as we can get away with without selecting too strongly for resistant cells. The basic facts are that in a heterogeneous tumor (like most are), resistance is likely present before the application of the treatment. Also, in the case of chemotherapy, resistance comes at a cost to the resistant cell: the energy required to produce the pumps to discard the drug before it causes any harm would impact the cell’s proliferation.

With these two pieces of information, the idea is that ATs work by letting the tumor susceptible population recover from the treatment and limit the proliferation of the chemo-resistant cells. Basically you give up on the dream of completely eradicating the cancer in a patient for the more solid possibility of being able to control its growth and manage resistance.

During my meeting in Barcelona, a few days ago, I met with researchers working on managing the emergence of resistance in a variety of fields including bacteria and agriculture. One of the atendees was Andrew Read, a biologist from Penn State with a distinctive Kiwi accent, working on infectious diseases. My understanding of the conversation was that he was not convinced that there was enough evidence that susceptible cells supress the growth of resistant ones. He (together with Silvie Huijben and Troy Day) posits that in managing diseases like malaria with existing drugs, relative fitness is not as important as absolute fitness.

Here is the logic, which feels rather intuitive: resistant cells may grow at a slower pace but if there are abundant resources and space and all the relevant action happens on the growing edge of the tumour then where’s the competition that will make sure resistance cells are kept in check?

The image that heads this post corresponds to a simulation image of a very simple agent-based model where every pixel represents a cell. The colours (mostly shades of grey) represent the degree of resistance (1-100) so that darker shades are less resistant and tad faster proliferators. As the tumour grows from the middle it becomes easy to see that:

1. Heterogeneity appears and given the weakness of selection is, to some extent, maintained.
2. The tumour gets darker as it grows showing that, over time, the faster proliferating/less resistant cells increase their proportion of the tumour burden.

The simulation can be seen more clearly here:

Average # of receptors over time as the tumor grows

As the above figure shows, our interpretation of the head figure is not misleading: as the tumor grows the average cell decreases in resistance potential and increases in proliferative potential.

Certainly not groundbreaking results but they help define our intuition of how even small differences in proliferation can lead to dominance of certain clones on the growing edge of a tumour. As we start with a cell with moderate amounts of resistance/growth (30/100), we see how faster proliferators (with values that quickly reach the low 10s and then 1) start occupying increasingly more of the space on the edge of the tumour. Thus limiting the proliferation of cells that have more resistance. This is taking into consideration that mutations are relatively rare (1%) and very incremental (they change resistance/growth by 1 unit). Why is this important? without that dominance in the tumour’s growing edge, ATs are a non-starter. We will see soon why this is important.

Code for this quick and dirty model can be found in my github.

EGT Reading Group 51 – 55 and a photo

We are busy at CancerEvo, read what Artem wrote about the reading group he organizes: Source: EGT Reading Group 51 – 55 and a photo

Congrats to Raj Warman!

Raj Warman, our high school student intern has been accepted to study at Yale University starting next academic year. Congrats Raj! Let the math modeling force be with you!